Космологическое красное смещение - что это такое

Пожалуй, одним из самых главных наблюдаемых параметров всех космологических объектов является так называемое красное смещение, на основании которого сделан вывод о расширении Вселенной. Суть этого явления в космологии состоит в смещении линий спектра излучения светящихся объектов в сторону более длинных волн. Известно, что возбужденные атомы разреженных газов или паров, которые могут возникнуть при нагревании любого химического элемента, испускают свет, разложение которого на призме образует линейчатый спектр, состоящий из отдельных цветных линий. При этом каждый химический элемент имеет характерный именно для него линейчатый спектр. Вызвано это тем, что атомы таких элементов, изолированные друг от друга, излучают свет только определенных длин волн. Эти волны имеют строго определённые резонансные частоты, которые в специальных приборах — спектроскопах — видны как темные или светлые линии в определённых частях спектра, характерных именно для этого вещества. Сдвиг этих исходных спектральных линий химических элементов в сторону более длинных волн, в "красную" сторону и называется красным смещением. В космологии красное смещения обозначают через z и определяют его как относительный прирост длины  волны: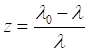



   В более общем виде это уравнение записывают следующим образом:
"…
 
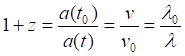
   Все величины, помеченные индексом 0, относятся к моменту приёма волны t0 > t. Так как в расширяющейся Вселенной a(t0) > a(t), то z > 0 и длина волны принимаемого сигнала больше, чем излучённого. Величина z = ( λ0--λ)/ λ, называемая параметром красного смещения, равна относительному увеличению длины волны принимаемого электромагнитного сигнала" [4].

   Величина красного смещения зависит от относительной скорости движения объектов — передатчика, генератора волны, и получателя, поэтому красное смещение позволяет определить эту относительную скорость. Вместе с тем, функциональная зависимость между скоростью и красным смещением нередко приводится в разных вариантах:
   "Смещение линий в спектре небесного тела к красному концу (в сторону большей длины волны) в результате эффекта Доплера при удалении тела, а также под действием его гравитационного поля. Численно красное смещение обычно характеризуют величиной z=(λ — λ0)/λ0, где λ — длина волны спектральной линии в излучении, приходящем от космического источника; λ0 — длина волны той же линии, измеренная в спектре неподвижного лабораторного источника. При небольших скоростях движения эффект Доплера вызывает красное смещение (или голубое, если источник приближается к наблюдателю), пропорциональное лучевой скорости (v): z = v/c, где c — скорость света. При v ~ c эта зависимость становится сложнее" [7]:




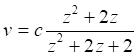
   Приведённое в цитируемой заметке выражение в литературе нередко имеет иной вид:

 
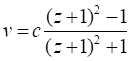
   Заметим, что в двух последних цитатах обозначения длин волн имею противоположную индексацию, но по смыслу они тождественны. Приведённые диапазоны применимости красного смещения и соответствующие им уравнения в литературе встречаются повсеместно, однако их обоснование в широком доступе отсутствует. Во-первых, из каких соображений выведено уравнение, связывающее скорости и красное смещение при больших скоростях? Во-вторых, из чего следуют диапазоны их корректных соотношений?
   Обзор физической литературы показал, что эффект Доплера, лежащий в основе традиционного красного смещения, к космологическому красному смещению нигде в общедоступной литературе явным образом не привязывается. Описание эффекта зачастую приводится в довольно общем виде. Например, [5, с.159]:
   "... α — угол … между направлением испускания волны и направлением движения — источника, и выражая ω через ω0, получим:


 
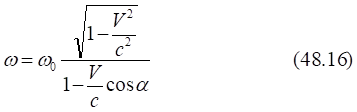
   Здесь ω — это угловая частота ("частота волны"), которая к космологии имеет, очевидно, косвенное отношение. Непосредственно в этом уравнении не просматриваются ни расширение пространства Вселенной и скорости удаления галактик друг от друга, ни скорость линейного удаления источника и получателя излучаемой волны. Похожие уравнения приводятся и в других изданиях [8, 3].
   Можно встретить и иные формальные выкладки, ведущие к выражению для связи красного смещения и скорости удаления объектов. Например, в работе [2, с.1509] приводится уравнение, из которого и выводится известное выражение для красного смещения:



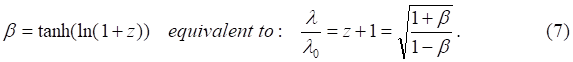
   Действительно, тривиальные преобразования этих уравнений приводят к уравнению выше:



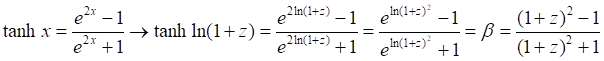
   И, наконец:

 
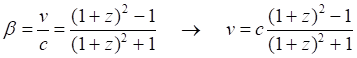
   Вместе с тем, отметим, что происхождение исходного выражения в цитируемом источнике описывается довольно замысловато, причём с позиции, отвергающей саму идею Большого Взрыва, расширения пространства и закона Хаббла:
   "Представлен анализ ошибочного происхождения так называемого закона скорости Хаббла… В настоящее время широко распространенный взгляд объясняет космологическое красное смещение, используя расплывчатую концепцию расширения физического пространства. Например, наблюдения говорят нам, что пространство внутри галактик, которые являются довольно рассеянными объектами, не расширяется. Тогда где находится "граница" в пространстве, которая разделяет расширяющееся пространство от нерасширяющегося? Далее нам говорят, что само расширение (инфляция) происходит из-за какого-то довольно таинственного события, которое было саркастически названо Фредом Хойлом (чтобы высмеять всю концепцию), как большой взрыв. Вместо этого мы предлагаем альтернативное решение, основанное на простой геометрии Лобачевского" [2, с.1518].
   Хотя происхождение классического выражения закона Хаббла и объявлено ошибочным, тем не мене, "правильный" вывод, альтернативное решение приводит именно к используемому в классическом законе Хаббла уравнению красного смещения. Кроме того заметим, что это альтернативное решение является, по сути, решением геометрическим, а не физическим, и никак не объясняет физической сути красного смещения.
   В работе [6] хотя и приводится весьма детальный анализ эффекта. Однако такая, по сути, чрезмерная детализация и обилие различных переменных затрудняют понимание изложенного материала.
   В формализме специальной теории относительности в основе космологического красного смещения лежит эффект Доплера, изменение длины волны излученного источником света или, соответственно, его частоты при его получении приёмником (наблюдателем), если он движется относительно источника [8]. Понятно, что наблюдение изменения частоты (длины волны) в принципе возможно только в одном случае: когда известны их исходные значения. Когда приёмник, наблюдатель регистрирует некоторое излучение, он получает конкретные значения этих величин, которые в момент регистрации о своих исходных значениях не несут никакой информации.
   Относительно детальный вывод уравнений для определения скорости удаляющегося объекта по его красному смещению, по доплер-эффекту приведён в википедии:
   "Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны λ) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется - длина волны увеличивается:

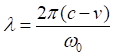    (0)
 
   где ω0 - угловая частота, с которой источник испускает волны, c - скорость распространения волн в среде, v  — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется). Частота, регистрируемая неподвижным приёмником

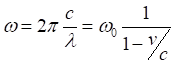     (1)
 
   ... В случае распространения электромагнитных волн (или других безмассовых частиц) в вакууме, формулу для частоты выводят из уравнений специальной теории относительности. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя …

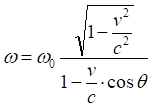     (4)
 
   где c - скорость света, v  — скорость источника относительно приёмника (наблюдателя), θ - угол между направлением на источник и вектором скорости в системе отсчёта приёмника. Если источник радиально удаляется от наблюдателя, то θ = π, если приближается, то θ = 0. Если пренебречь малыми по v/c второго порядка, то релятивистская формула сводится к классическому эффекту Доплера" [8].
   Из этого уравнения (4) можно вывести соотношение между скоростью и красным смещением. В цитате мы добавили номера к формулам (0), (1) и (4), которые в оригинале отсутствуют. Если взять левое равенство уравнения (1) из приведённой цитаты:

 
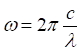
   и использовать его для подстановки в уравнение (4), рассматривая движение света и объектов вдоль одной линии, при котором θ = π (источник и приёмник удаляется друг от друга), и традиционно приняв с = 1, получим:



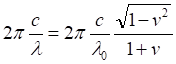
   После сокращения получаем:



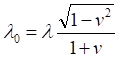
   Учитывая уравнение для красного смещения:
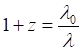     (5)


   находим:



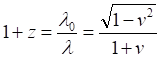
   После сокращения получаем:
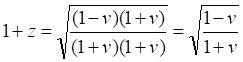     (6)
 
   Строго говоря, это уравнение для красного смещения не должно иметь решений, поскольку при любой скорости величина смещения z оказывается отрицательной величиной:




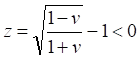
   Тем не менее, решая это уравнение, находим зависимость скорости от красного смещения:



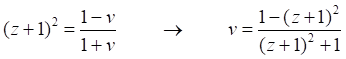
   Или в традиционной развёрнутой форме:
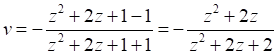     (7)
 
   Странный знак минус с неясными обоснованиями следует отбросить. Из исправленного уравнения, отбрасывая величины высших порядков малости, можно получить традиционное уравнение приближенных значений скорости для z << 1

 
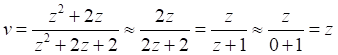
   Нередко в литературе указывается, что такое приближение допустимо при красных смещениях до величины порядка z ~ 0,1 [7]. Однако такое приближение сделано "на глазок". Разумнее выяснить, как зависит погрешность вычисления скорости от красных смещений. Точное значение скорости определяется уравнением (7). Переход к приближённому уравнению связи красного смещения и скорости v = cz может быть произведён также отбрасыванием членов высшего порядка через разложение Тейлора, как это описано в [1, с.406]:




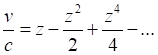
   Погрешность вычисления скорости с её завышением при таком отбрасывании и значении z = 0,1 составляет 5%:



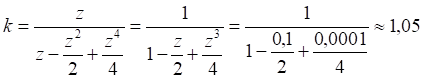
   Более точно величину погрешности можно найти из следующих соображений. Пусть приближенное значение скорости отличается от точного значения на множитель k < 1, то есть:



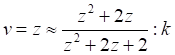
   Тогда
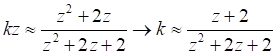     (8)


   Преобразуем:



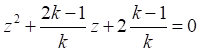
   Уравнение позволяет вычислить, при каких z погрешность не будет превышать величину k. В частности, для k = 1 находим:

 
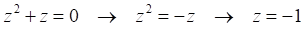
   Это решение, очевидно, неприемлемо, поскольку по определению красное смещение при разбегании участников положительно. Для других значений приближения погрешность можно найти из уравнения (8). Например, погрешности для значений z = 0,01 и z = 0,1 равны:






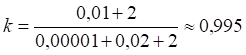
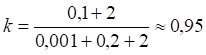
   Как видим, действительно, при значениях z < 0,1 погрешность вычисления скорости не превышает 5%. Если же z > 1, то погрешность превышает 40%:

 
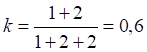
   Следует заметить, что в приведённой выше цитате уравнение (0), предшествующее уравнению (1), описано несколько двусмысленно. Не совсем понятно, относится оно к случаю, когда "источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается", либо к случаю, когда он "удаляется - длина волны увеличивается". По смыслу уравнения (0) и (1) соответствуют случаю сближения источника и приёмника. Кроме того и сами утверждения уменьшается-увеличивается также недостаточно наглядны. Поэтому рассмотрим эти изменения длины волны в более развернутом виде. На рисунке показано, что при движении световой волны мимо наблюдателя, неподвижного относительно источника, v = 0, наблюдатель за одну секунды фиксирует некоторое количество периодов этой волны:




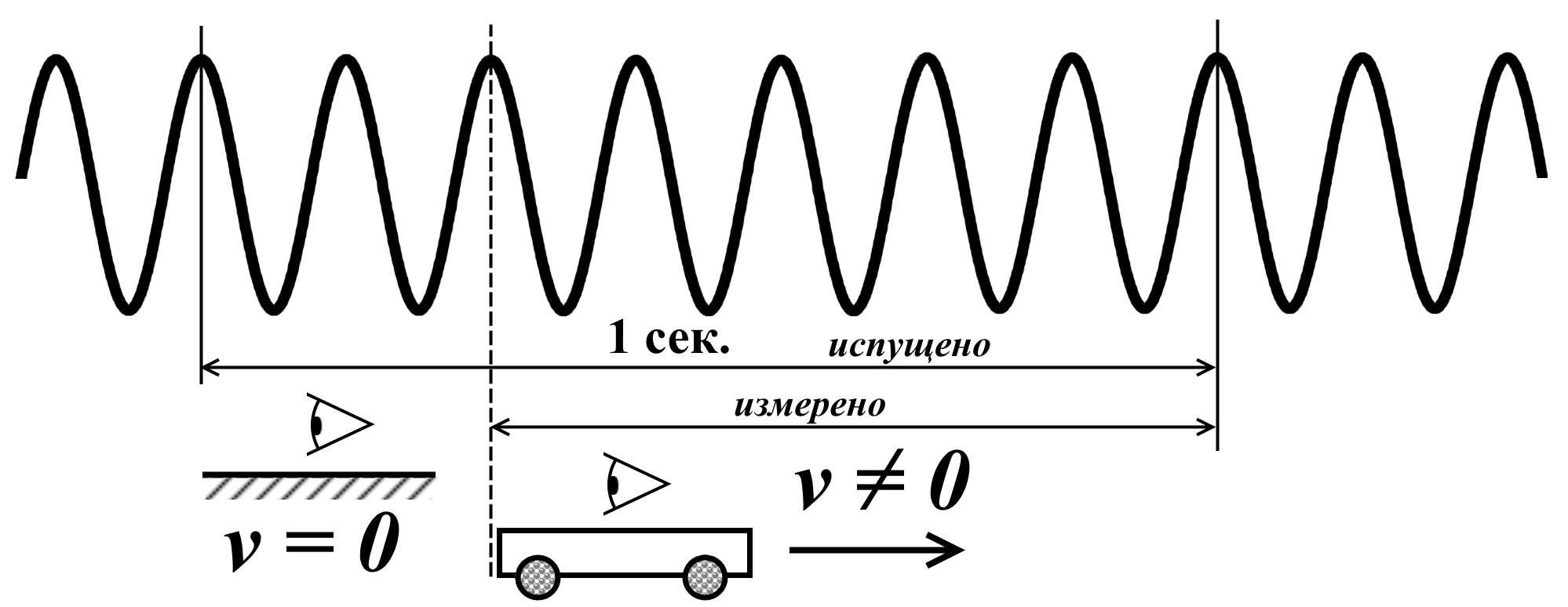
Рис.1. Удаляющийся наблюдатель фиксирует меньшее число периодов волны
 
   Очевидно, и не требует отдельных доказательств, что измеренная длина волны для неподвижного наблюдателя равна излученной длине волны λизл. В этом случае приёмник, наблюдатель зафиксирует количество колебаний, равное:



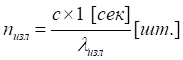
   где
   nизл — количество подсчитанных колебаний, а индекс означает принадлежность источнику.
  
   В уравнении умноженная на 1 секунду скорость света — это путь, пройденный за 1 секунду пересчитанными колебаниями с длиной волны λизл. Если же получатель, приёмник удаляется от излучателя, что соответствует расширяющейся Вселенной, то, как видно на рисунке, за эту же секунду он насчитает меньшее количество колебаний, периодов световой волны. За эту секунду относительно наблюдателя, приёмника волна пройдёт меньший путь, поскольку приёмник переместился, двигаясь со скоростью v, поэтому наблюдатель и насчитает меньшее число nнаб периодов λ:


 
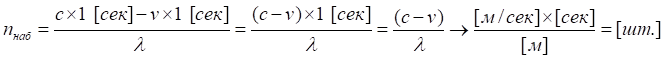
   Все эти периоды подсчитаны за то же время — 1 секунду, что "видно" с точки зрения излучателя (источника). Действительно, наблюдая за движущимся наблюдателем, приёмником, он однозначно фиксирует, что тот пересчитал именно такое количество "периодов" волны. Из этого следует, что при световой скорости движения волны этому количеству периодов nнаб соответствует и большее значение длины волны (длины её одного периода). В самом деле, за 1 секунду мимо движущегося наблюдателя пробежало nнаб штук периодов общей длиной, равной пути, пройденному светом за это же время, 1 секунду. Следовательно, фактическая длина волны с точки зрения движущегося (да и неподвижного) наблюдателя равна:


 
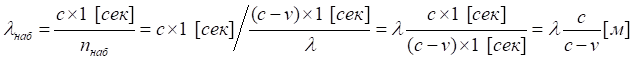
   Это, очевидно, верное соотношение. Действительно, если v = 0, то длина наблюдаемой волны равна длине излучаемой. Иначе, при удалении наблюдателя от источника, длина наблюдаемой волны всегда больше длины излучаемой. Напротив, при сближении, отрицательном значении скорости, длина волны оказывается меньше излученной. Если подставить эти значения длин волн в уравнение для красного смещения, то получим:


 
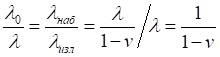
   Соотношение выглядит корректным, поскольку, действительно, при удалении приёмника вычисленная по нему длина волны λнаб всегда больше излученной. Иначе, при нулевой скорости они равны, а при сближении (скорость отрицательна) вычисленная длина волны λнаб всегда оказывается меньше излученной. Однако здесь мы обязаны учесть ещё один эффект — лоренцево сокращение длины. Поскольку измеряемый участок волны как физический объект движется относительно неподвижного наблюдателя, его внутренняя линейка сокращается относительно неподвижной линейки наблюдателя. Это прямо следует из принципа относительности: если приемник движется относительно источника с некоторой скоростью, то это тождественно тому, что и источник движется с той же скоростью относительно приёмника. Поскольку нас интересует картина с точки зрения приёмника, то мы и принимаем, что именно источник движется относительно него. Из этого следует, что движущемуся наблюдателю длина волны и связанная с источником и движущаяся вместе с ним линейка видятся более короткими:


 
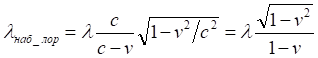
   Буквально это означает, что наблюдатель видит сократившуюся волну. Несмотря на это лоренцево сокращение, мы вновь отмечаем корректность полученного соотношения: при любом значении скорости наблюдаемая движущимся приёмником длина волны всегда больше излученной длины волны, поскольку величина дроби всегда больше единицы:




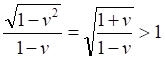
   При нулевой скорости длины сравниваемых волн равны:



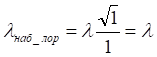
   И, наоборот, при сближении участников, когда скорость отрицательна, наблюдаемая длина волны всегда меньше излученной:



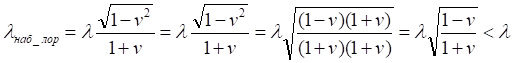
   Таким образом, в соответствие с принятыми выше обозначениями, находим:

 
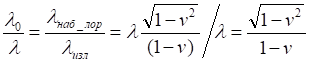
   Как видим, полученное соотношение явно не совпадает с уравнением (6), полученным из уравнений приведённой цитаты, однако традиционное конечное уравнение из него выводится строго корректно [3, с.5]:



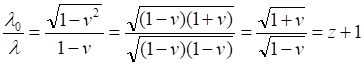
   Преобразовав последнее равенство в уравнении, находим:



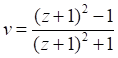
   Если раскрыть скобки, то получим другой известный вариант этого уравнения:



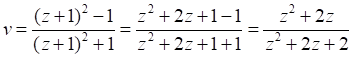
   Отсюда можно сделать вывод, что, по всей видимости, в цитате [8] содержится неточность: в знаменателе уравнения (4) должен стоять знак плюс. Эту же неточность следует отметить и в уравнении (48.16) [5, с.159].
  
  
   Литература
   1. Bedran M.L., A comparison between the Doppler and cosmological redshifts, Am. J. Phys. 70 (4), 2002.
   2. Brzeski J.G. (J. Georg von Brzeski), Expansion of the Universe — mistake of Edvin Hubble? Cosmological redshift and related electromagnetic phenomena in static Lobachevskian (hyperbolic) Universe. Acta physica polonica B, No.6, Vol.39 (2008). URL: https://www.actaphys.uj.edu.pl/fulltext?series=Reg&vol=39&page=1501
   3. Gray R., Dunning-Davies J., A review of redshift and its interpretation in cosmology and astrophysics. Department of Physics, University of Hull, Hull HU6 7RX, England
   4. Космологическое красное смещение, Википедия, URL: https://ru.wikipedia.org/wiki/Космологическое_красное_смещение
   5. Ландау Л. Д., Лифшиц Е. М. Теория поля. -- Издание 7-е, исправленное. -- М.: Наука, 1988. -- С. 158--159. -- ("Теоретическая физика", том II). -- ISBN 5-02-014420-7.
   6. Степанов С.С., Эффект Доплера, 2017, URL:
http://synset.com/ru/Эффект_Доплера
http://synset.com/pdf/phys_v1.pdf, с.80
   7. Сурдин В.Г., Красное смещение, ГАИШ, Москва, URL: http://www.astronet.ru/db/msg/1177975
   8. Эффект Доплера, Википедия, URL: https://ru.wikipedia.org/wiki/Эффект_Доплера